Logica Parte 2

- Equivalencia Logica

En lógica, las declaraciones p y q son lógicamente equivalentes si tienen el mismo contenido lógico. Este es un concepto semántico, dos afirmaciones son equivalentes si tienen el mismo valor de verdad en todos los modelos (Mendelson 1979:56). La equivalencia lógica de p y q algunas veces se expresa como ${\displaystyle p\equiv q}$, Epq, o ${\displaystyle p\Leftrightarrow q}$que Se expresa:

-Leyes Logicas

Para la simplificación de fórmulas del cálculo proposicional, son de suma utilidad las equivalencias o leyes lógicas. Su demostración se reduce a la confección de las correspondientes tablas de verdad (el resultado final de las mismas, siempre muestra una tautología). En la elaboración de las siguientes leyes, se ha supuesto que p, q y r son proposiciones que pueden asumir cualquier valor de verdad; mientras que V es una proposición verdadera y F es una proposición falsa. 

1-Introducción de la negación

De ${\displaystyle (p\to q)}$ y ${\displaystyle (p\to \neg q)}$, se infiere ${\displaystyle \neg p}$.

Esto es, ${\displaystyle \{(p\to q),(p\to \neg q)\}\vdash \neg p}$.

2-Eliminación de la negación

De ${\displaystyle \neg p}$, se infiere ${\displaystyle (p\to r)}$.

Esto es, ${\displaystyle \{\neg p\}\vdash (p\to r)}$.

3-Eliminación de la doble negación

De ${\displaystyle \neg \neg p}$, se infiere ${\displaystyle p}$.

Esto es, ${\displaystyle \neg \neg p\vdash p}$.

4-Introducción de la conjunción

De ${\displaystyle p}$ y ${\displaystyle q}$, se infiere ${\displaystyle (p\land q)}$.

Esto es, ${\displaystyle \{p,q\}\vdash (p\land q)}$.

5-Eliminación de la conjunción

De ${\displaystyle (p\land q)}$, se infiere ${\displaystyle p}$.

De ${\displaystyle (p\land q)}$, se infiere ${\displaystyle q}$.

Esto es, ${\displaystyle (p\land q)\vdash p}$ y ${\displaystyle (p\land q)\vdash q}$.

6-Introducción de la disyunción

De ${\displaystyle p}$, se infiere ${\displaystyle (p\lor q)}$.

Esto es, ${\displaystyle p\vdash (p\lor q)}$ y ${\displaystyle q\vdash (p\lor q)}$.

7-Eliminación de la disyunción

De ${\displaystyle (p\lor q)}$ y ${\displaystyle (p\to r)}$ y ${\displaystyle (q\to r)}$, se infiere ${\displaystyle r}$.

Esto es, ${\displaystyle \{p\lor q,p\to r,q\to r\}\vdash r}$.

8-Introducción del bicondicional

De ${\displaystyle (p\to q)}$ y ${\displaystyle (q\to p)}$, se infiere ${\displaystyle (p\leftrightarrow q)}$.

Esto es, ${\displaystyle \{p\to q,q\to p\}\vdash (p\leftrightarrow q)}$.

9-Eliminación del bicondicional

De ${\displaystyle (p\leftrightarrow q)}$, se infiere ${\displaystyle (p\to q)}$.

De ${\displaystyle (p\leftrightarrow q)}$, se infiere ${\displaystyle (q\to p)}$.

Esto es, ${\displaystyle (p\leftrightarrow q)\vdash (p\to q)}$ y ${\displaystyle (p\leftrightarrow q)\vdash (q\to p)}$.

10-Modus ponens (eliminación del condicional)

De ${\displaystyle p}$ y ${\displaystyle (p\to q)}$, se infiere ${\displaystyle q}$.

Esto es, ${\displaystyle \{p,p\to q\}\vdash q}$.

11-Prueba condicional (introducción del condicional)

De [aceptando que ${\displaystyle p}$ permite una prueba de ${\displaystyle q}$], se infiere ${\displaystyle (p\to q)}$.

Esto es, ${\displaystyle (p\vdash q)\vdash (p\to q)}$

-Simplicacion de Formulas Proposiconales

La simplificación de una proposición, dicho de otra manera, lasimplificación de una expresión lógica consiste en reducir la expresiónlógica aúna forma más simple mediante el uso de los axiomas/o leyes lógicas. La simplificación consiste en ir desarrollando la expresión pasa mediante la sustitución en cada paso de una expresión lógica equivalente ala anterior, hasta llegara una expresión lógica irreducible. A través de la simplificación podemos también demostrar unaequivalencia lógica sin usar tablas de verdad.

Ejemplos:

-Conectivos Logicos

En lógica, una conectiva lógica, o también conectiva (también llamado operador lógico o conectores lógicos) es un símbolo o palabra que se utiliza para conectar dos fórmulas bien formadas o sentencias (atómicas o moleculares), de modo que el valor de verdad de la fórmula compuesta depende del valor de verdad de las fórmulas componentes. Los conectivos lógicos más comunes son los conectivos binarios (también llamados conectivos diádicos) que unen dos frases, que pueden ser consideradas los operandos de la función. También es común considerar a la negación como un conectivo monádico.

-Logica de Bits (not, and, or ,xor)

-Compuertas Logicas y Algebra de  Boole

Las Compuertas Lógicas son circuitos electrónicos conformados internamente por transistores que se encuentran con arreglos especiales con los que otorgan señales de voltaje como resultado o una salida de forma booleana, están obtenidos por operaciones lógicas binarias (suma, multiplicación).

Compuerta AND

Esta compuerta es representada por una multiplicación en el Algebra de Boole. Indica que es necesario que en todas sus entradas se tenga un estado binario 1 para que la salida otorgue un 1 binario. En caso contrario de que falte alguna de sus entradas con este estado o no tenga si quiera una accionada, la salida no podrá cambiar de estado y permanecerá en 0. Esta puede ser simbolizada por dos o más interruptores en serie de los cuales todos deben estar activos para que esta permita el flujo de la corriente.

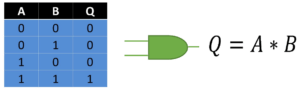
Fig. 2 Tabla, Representación y Fórmula Compuerta AND.

Compuerta OR

En el Algebra de Boole esta es una suma. Esta compuerta permite que con cualquiera de sus entradas que este en estado binario 1, su salida pasara a un estado 1 también. No es necesario que todas sus entradas estén accionadas para conseguir un estado 1 a la salida pero tampoco causa algún inconveniente. Para lograr un estado 0 a la salida, todas sus entradas deben estar en el mismo valor de 0. Se puede interpretar como dos interruptores en paralelo, que sin importar cual se accione, será posible el paso de la corriente.

Fig. 3 Tabla, Representación y Fórmula Compuerta OR.

Compuerta NOT

En este caso esta compuerta solo tiene una entrada y una salida y esta actúa como un inversor. Para esta situación en la entrada se colocara un 1 y en la salida otorgara un 0 y en el caso contrario esta recibirá un 0 y mostrara un 1. Por lo cual todo lo que llegue a su entrada, será inverso en su salida.

Fig. 4 Tabla, Representación y Fórmula Compuerta NOT.

Compuerta NAND

También denominada como AND negada, esta compuerta trabaja al contrario de una AND ya que al no tener entradas en 1 o solamente alguna de ellas, esta concede un 1 en su salida, pero si esta tiene todas sus entradas en 1 la salida se presenta con un 0.

Fig. 5 Tabla, Representación y Fórmula Compuerta NAND.

Compuerta NOR

Así como vimos anteriormente, la compuerta OR también tiene su versión inversa. Esta compuerta cuando tiene sus entradas en estado 0 su salida estará en 1, pero si alguna de sus entradas pasa a un estado 1 sin importar en qué posición, su salida será un estado 0.

Fig. 6 Tabla, Representación y Fórmula Compuerta NOR.

Compuerta XOR

También llamada OR exclusiva, esta actúa como una suma binaria de un digito cada uno y el resultado de la suma seria la salida. Otra manera de verlo es que con valores de entrada igual el estado de salida es 0 y con valores de entrada diferente, la salida será 1.

Fig. 7 Tabla, Representación y Fórmula Compuerta XOR.

Compuerta XNOR

Esta es todo lo contrario a la compuerta XOR, ya que cuando las entradas sean iguales se presentara una salida en estado 1 y si son diferentes la salida será un estado 0.

Fig. 8 Tabla, Representación y Fórmula Compuerta XNOR.

Compuerta IF

Esta compuerta no es una muy utilizada o reconocida ya que su funcionamiento en estados lógicos es parecido a si solo hubiera un cable conectado porque exactamente lo que se le coloque en la entrada, se encontrara en la salida. Pero también es conocido como un buffer, en la práctica se utiliza como amplificador de corriente o como seguidor de tensión para adaptar impedancias.

-Mapa de Karnaugh

Un mapa de Karnaugh (también conocido como tabla de Karnaugh o diagrama de Veitch, abreviado como Mapa-K o Mapa-KV) es un diagrama utilizado para la simplificación de funciones algebraicas Booleanas. El mapa de Karnaugh fue inventado en 1953 por Maurice Karnaugh, un físico y matemático de los laboratorios Bell.

Los mapas de Karnaugh reducen la necesidad de hacer cálculos extensos para la simplificación de expresiones booleanas, aprovechando la capacidad del cerebro humano para el reconocimiento de patrones y otras formas de expresión analítica, permitiendo así identificar y eliminar condiciones muy inmensas.

El mapa de Karnaugh consiste en una representación bidimensional de la tabla de verdad de la función a simplificar. Puesto que la tabla de verdad de una función de N variables posee 2N filas, el mapa K correspondiente debe poseer también 2N cuadrados. Las variables de la expresión son ordenadas en función de su peso y siguiendo el código Gray, de manera que sólo una de las variables varía entre celdas adyacentes. La transferencia de los términos de la tabla de verdad al mapa de Karnaugh se realiza de forma directa, albergando un 0 o un 1, dependiendo del valor que toma la función en cada fila. Las tablas de Karnaugh se pueden fácilmente realizar a mano con funciones de hasta 6 variables, para funciones de mayor cantidad de variables es más eficiente el uso de software especializado.

-Grafos 

La teoría de grafos (también llamada teoría de las gráficas) es un campo de estudio de las matemáticas y las ciencias de la computación, que estudia las propiedades de los grafos

-Tipos de Grafos

-       Grafo simple: un grafo simple G = (V, E) constan de V, un conjunto no vacío de vértices, y de E, un conjunto de pares no ordenados de elementos distintos de V. A estos parea se llama aristas. Un grafo es simple si  una arista cualquiera es la única que une dos vértices específicos.

-       Grafo Multígrafo: un multígrafo G = (V, E) constan de un conjunto V de vértices, un conjunto E de arista, un función f de E. Se dice que las aristas e1 y e2.son aristas múltiples o palearlas si f (e1) = f (e2).

Pseudografo: un pseudografo G = (V, E) constan de un conjunto V de vértices y un conjunto E de arista, un función f de E. una arista e es un bucle o lazo, si f (e) = (u, u) = (u) para algún u e V. Esto quiere decir que un Pseudografo exista un es aquel multigrafío en donde al menos bucle (un vértice conectado con si mismo).

-       Grafo dirigido: un grafo dirigid (V, E) constan de un conjunto V de vértices y un conjunto E de arista, que son pares ordenados de elementos de V.

-       Multígrafo dirigido: un multígrafo dirigido G = (V, E) constan de un conjunto V de vértices y un conjunto E de arista, un función f de E. se distingue una aristas múltiples si f (e1) = f (e2).